« Et si l’univers ne se courbait pas — mais tenait simplement la mesure du temps ? »
— Modèle de Gravité du Vide, 2025
Cet essai présente le Modèle de Gravité du Vide (VGM) — un cadre théorique sans métrique où la gravitation, l’inertie et le flux du temps émergent de variations mesurables d’un champ scalaire unique : la cadence du vide.
Plutôt que de courber l’espace-temps, le vide en modifie le tempo.
Les prédictions de la Relativité Générale y apparaissent comme des limites du premier ordre, tandis que le modèle prévoit une rigidité à portée finie et une accélération cosmique de type Born–Infeld.
Il propose ainsi un passage de la géométrie à la métrologie : la gravitation devient la comparaison des rythmes plutôt que celle des formes, suggérant que l’univers ne se courbe peut-être pas — il bat.
La beauté et les limites de la courbure
Depuis plus d’un siècle, la Relativité Générale demeure l’une des idées les plus puissantes et les plus élégantes de l’histoire de la science. D’un seul principe géométrique — « la matière dit à l’espace comment se courber, et l’espace dit à la matière comment se mouvoir » — Einstein transforma la gravitation, force invisible, en la forme même du réel. Des mouvements planétaires aux ondes gravitationnelles issues de la fusion des trous noirs, chaque prédiction a été confirmée avec une précision stupéfiante. Lorsque les astrophysiciens observent que les ondes gravitationnelles se propagent à la vitesse de la lumière, ils confirment en réalité que la géométrie elle-même peut vibrer.
Pourtant, derrière ce triomphe se cache une question silencieuse qu’Einstein n’a jamais totalement résolue : qu’est-ce qui se courbe, au juste ? La relativité décrit comment l’espace-temps se comporte, mais non de quoi il est fait. La théorie confère à la géométrie une vie dynamique, mais laisse indéfini le matériau de cette scène cosmique. Entre la courbure continue de la Relativité Générale et le vide quantique agité de la théorie des champs s’ouvre un gouffre conceptuel : la première décrit un continuum parfaitement lisse, tandis que le second foisonne de discontinuités.
Cette tension n’est pas anodine. Elle nourrit chaque paradoxe à la frontière entre gravitation et mécanique quantique : entropie des trous noirs, accélération cosmique, constante cosmologique. La Relativité Générale triomphe partout où la géométrie reste douce, mais elle chancelle là où la structure microscopique de l’espace devrait se révéler. Ses équations décrivent comment la courbure répond à l’énergie, mais non quelle propriété physique du vide fixe la cadence des horloges, la trajectoire de la lumière ou l’inertie de la matière. Demander ce qui se courbe, c’est en réalité interroger la nature du vide lui-même.
Et si la géométrie n’avait jamais été l’acteur fondamental, mais seulement le langage employé pour décrire un phénomène plus profond ? La prochaine étape serait alors de regarder sous la surface du décor : chercher une substance mesurable du vide, un champ dont les variations engendreraient ce que nous percevons comme la courbure. Si un tel substrat existe, la gravitation ne serait plus la déformation de l’espace, mais la réponse d’un milieu invisible à l’énergie et au mouvement. La question que pose cette approche est simple et radicale :
Et si la géométrie de l’espace-temps n’était que l’ombre d’un état physique du vide ?
La question cachée : de quoi le vide est-il fait ?
Si la géométrie n’est que la scène sur laquelle la matière se déplace, de quoi cette scène est-elle donc constituée ?
Dans les équations d’Einstein, la réponse demeure purement mathématique : l’espace-temps est un tissu continu dont la courbure traduit la présence de gravité. Mais la physique moderne murmure tout autre chose : le vide n’est pas vide.
La théorie quantique des champs le peuple d’une énergie inépuisable : fluctuations du champ apparaissant et disparaissant sans cesse, condensats éphémères surgissant dans l’infiniment bref des attosecondes. Ce « vide quantique » se comporte moins comme un néant que comme un océan dont la tension de surface déterminerait les lois mêmes de la nature.
Or cette image se heurte à une contradiction vertigineuse : le vide quantique devrait peser des milliards de fois plus que l’univers ne le supporte.
En additionnant les énergies de point zéro de tous les champs connus, on obtient une densité d’énergie ![]() fois trop grande.
fois trop grande.
Pour rendre les équations d’Einstein compatibles avec les observations, il faut donc introduire une constante artificielle — la fameuse constante cosmologique — sans doute le réglage le plus déroutant de toute la physique moderne.
C’est comme si le vide bruissait si fort qu’il fallait ajuster les équations jusqu’au silence pour que les galaxies puissent exister.
Depuis des décennies, les physiciens soupçonnent que la clé manquante ne viendrait pas nécessairement d’une nouvelle particule, mais d’un principe encore inconnu — et peut-être du vide lui-même.
Le substrat du vide est peut-être tout sauf inerte ou figé : il pourrait au contraire être hautement énergétique, fluide et dynamique, capable de se tendre, d’osciller ou de se détendre comme un milieu élastique dont dépendraient la matière, le mouvement et la trame même de l’univers.
Cette interrogation — de quoi le vide est-il fait ? — marque la frontière mouvante entre le connu et le spéculatif. De la « gravité induite » de Sakharov aux modèles entropiques de Verlinde ou aux analogies superfluides contemporaines, chaque tentative a cherché l’origine physique de la métrique elle-même.
Le Modèle de Gravité du Vide (VGM) s’inscrit dans cette lignée en y ajoutant une inflexion décisive : il identifie un champ scalaire unique, mesurable, dont les variations locales reproduisent toutes les prédictions testées de la Relativité Générale tout en demeurant fondamentalement sans métrique.
Dans cette perspective, gravitation, inertie et temps ne sont plus des attributs de la courbure, mais les réponses d’un vide structuré à l’énergie et au mouvement.
Peut-être le mystère le plus profond de la physique moderne n’est-il pas que l’espace-temps se courbe, mais qu’il témoigne des battements du vide — comme le cardiogramme d’un univers vivant. Pour comprendre la gravitation, il faut donc apprendre non pas comment l’univers se plie, mais comment son vide bat.
La notion de cadence du vide
Imaginons que le vide lui-même possède un rythme — une oscillation silencieuse qui règle la mesure de toute horloge et la résistance de toute masse.
C’est là le cœur du Modèle de Gravité du Vide (VGM) : gravitation, inertie et écoulement du temps émergent de variations locales d’une unique grandeur scalaire mesurable — le champ de cadence, généralement noté ![]() .
.
Plutôt que de décrire comment la géométrie se courbe, le VGM décrit comment le tempo interne du vide varie d’un point à l’autre.
En termes simples, le champ ![]() mesure la tension inertielle du vide.
mesure la tension inertielle du vide.
Là où ![]() augmente, les horloges ralentissent et les ondes lumineuses s’étirent ; ce que nous appelons décalage gravitationnel vers le rouge n’est alors que le reflet d’un changement de rythme du vide.
augmente, les horloges ralentissent et les ondes lumineuses s’étirent ; ce que nous appelons décalage gravitationnel vers le rouge n’est alors que le reflet d’un changement de rythme du vide.
Là où ![]() diminue, le temps s’accélère et la lumière gagne en fréquence.
diminue, le temps s’accélère et la lumière gagne en fréquence.
Chaque potentiel gravitationnel, chaque accélération, chaque courbure de trajectoire peut ainsi se ramener à un gradient de cadence.
Dans sa limite faible, ![]() se comporte exactement comme le potentiel newtonien divisé par
se comporte exactement comme le potentiel newtonien divisé par ![]() , assurant la concordance complète avec tous les tests post-newtoniens de premier ordre de la Relativité Générale.
, assurant la concordance complète avec tous les tests post-newtoniens de premier ordre de la Relativité Générale.
Sous cet éclairage, la gravitation n’est plus une géométrie, mais une métrologie.
Une expérience gravitationnelle devient une comparaison de rythmes plutôt qu’une mesure de formes.
Une horloge atomique en orbite et une autre au sol ne se situent pas dans des positions différentes d’un espace courbé ; elles vivent dans des régions de cadence légèrement distincte.
L’équation ![]() exprime alors directement le principe d’équivalence : tous les corps, massifs ou non, répondent au même gradient scalaire, car tous participent du même rythme de vide.
exprime alors directement le principe d’équivalence : tous les corps, massifs ou non, répondent au même gradient scalaire, car tous participent du même rythme de vide.
Une telle description entraîne une conséquence inattendue : elle unifie gravitation, inertie et temps sous une seule loi observable.
L’accélération résulte du gradient spatial de la cadence ; l’inertie traduit la résistance du vide à toute variation de son rythme ; la dilatation du temps découle des fluctuations temporelles de ce même champ.
Les trois piliers de la physique classique — mouvement, masse, durée — se révèlent être les manifestations d’une même réalité : la dynamique du vide.
Sur le plan opérationnel, ce cadre ne renie pas la Relativité : il la reproduit à premier ordre et l’étend au-delà.
Le tenseur métrique d’Einstein devient alors un descripteur effectif, une façon pratique d’exprimer comment le champ de cadence influence horloges et étalons de longueur.
Mais la véritable variable dynamique est ![]() , un champ qui peut, en principe, être mesuré directement grâce à des réseaux d’horloges atomiques et à des expériences de chronométrie optique.
, un champ qui peut, en principe, être mesuré directement grâce à des réseaux d’horloges atomiques et à des expériences de chronométrie optique.
Là où Einstein dessine une courbure, le VGM enregistre une fréquence.
Si cette interprétation se vérifie, elle signifierait que la gravitation n’est pas une déformation de l’espace-temps, mais une modulation de la fréquence interne du vide — un battement physique inscrit au cœur de chaque processus cosmique.
L’univers, dans cette perspective, ne se courbe pas ; il bat la mesure.
De la géométrie à la métrologie : mesurer le rythme de l’espace
Si la gravitation est un rythme plutôt qu’une courbure, alors la physique devient un art d’écoute.
Il ne s’agit plus de cartographier des formes géométriques, mais de comparer des cadences : le battement des horloges, l’oscillation de la lumière, la respiration silencieuse du vide lui-même.
Dans cette perspective métrologique, chaque effet gravitationnel se ramène à une différence mesurable de fréquence — un décalage de cadence entre deux régions d’un même champ fondamental.
Einstein lui-même en avait déjà laissé l’intuition.
Le décalage vers le rouge de la lumière près d’un astre massif, le ralentissement des horloges terrestres par rapport à celles des satellites, ou encore la déviation des rayons lumineux au bord du Soleil, témoignent d’une même vérité : le temps ne s’écoule pas uniformément dans l’univers.
Dans le Modèle de Gravité du Vide (VGM), cette variation n’est plus une déformation des coordonnées, mais la modulation physique du champ de cadence ![]() .
.
Chaque horloge, chaque photon, participe de ce rythme universel, et leurs dérives relatives deviennent des sondes directes du gradient du champ.
Pour mesurer la gravitation, nul besoin d’un tenseur métrique : il suffit d’une comparaison de fréquences d’une précision extrême.
La physique moderne dispose déjà des instruments nécessaires à cette approche.
Des réseaux d’horloges optiques et micro-ondes, reliés par des faisceaux laser ou radio, mesurent des différences de rythme inférieures à une part sur ![]() .
.
Des missions spatiales telles que ACES, LATOR ou BepiColombo affinent ces mesures et transforment la gravitation en une branche de la métrologie de haute précision.
Dans le cadre du VGM, chaque observable — décalage gravitationnel, délai lumière-temps, déviation de la lumière, dérive cosmologique — correspond à l’un des cinq paramètres fondamentaux du vide :
![]()
Ces constantes définissent ensemble la rigidité, la vitesse de propagation et l’évolution lente de la cadence du vide.
Au premier ordre post-newtonien, les valeurs coïncident parfaitement avec celles d’Einstein :
![]()
Mais au-delà de ce seuil, le VGM introduit des corrections corrélées de second ordre — de légères déviations dans le délai de Shapiro, la précession du périhélie ou les interférences optiques — formant un motif falsifiable et cohérent.
Aucune constante arbitraire, aucune dimension cachée : seulement l’élasticité mesurable du vide lui-même.
En ce sens, le modèle ne renverse pas la Relativité Générale — il la calibre.
Une telle interprétation bouleverse la pratique même de la physique.
Si la géométrie cède la place à la cadence, théorie et mesure deviennent indissociables.
La gravitation se lit non plus dans la forme des trajectoires, mais dans la synchronisation des horloges.
Des ensembles d’horloges atomiques en orbite, des interféromètres optiques ou des spectres de galaxies lointaines deviennent les stéthoscopes du cosmos.
La carte future de la gravité ne ressemblera peut-être plus à une grille courbe de l’espace-temps, mais à un relief de fréquences, où chaque altitude représente le tempo local du vide.
Lorsque nous mesurons des différences de temps, nous entendons déjà le battement de l’univers.
L’étape suivante est de reconnaître que ce pouls est la gravitation elle-même.
L’univers élastique : rigidité et accélération cosmique
Si le vide règle vraiment le rythme de la gravitation, il doit aussi posséder une texture — une capacité à se tendre, à résister et à se détendre.
Dans le Modèle de Gravité du Vide (VGM), cette propriété s’appelle la rigidité : une réponse élastique finie du vide, qui transmet à la fois les effets gravitationnels locaux et la lente dérive cosmique de l’univers.
Là où la Relativité Générale considère la métrique comme parfaitement souple, le VGM confère au vide une raideur mesurable, caractérisée par deux paramètres : ![]() , sa longueur de cohérence, et
, sa longueur de cohérence, et ![]() , la vitesse de propagation de ses ondes internes.
, la vitesse de propagation de ses ondes internes.
Cette élasticité change tout.
Dans le régime de champ faible du Système solaire, le vide se comporte comme un milieu presque parfaitement flexible : sa rigidité effective est extrêmement faible, ce qui correspond à une longueur de corrélation ![]() immense.
Autrement dit, le vide réagit très lentement aux contraintes : ses gradients se développent sur de grandes distances, et la gravité y prend une forme douce et presque newtonienne.
Le champ de cadence se propage alors librement, comme des rides à la surface d’un océan trop vaste pour qu’on en perçoive la tension.
immense.
Autrement dit, le vide réagit très lentement aux contraintes : ses gradients se développent sur de grandes distances, et la gravité y prend une forme douce et presque newtonienne.
Le champ de cadence se propage alors librement, comme des rides à la surface d’un océan trop vaste pour qu’on en perçoive la tension.
À plus grande échelle — galactique ou cosmologique — ce même paramètre se raccourcit à mesure que le vide se tend et se raidit localement : ses gradients deviennent plus abrupts, sa réponse plus vive, et la gravité plus marquée —comme si la tension du vide dessinait, autour de masses extrêmes, comme une ombre de matière invisible.
L’équation différentielle qui décrit ![]() prend alors la forme d’une loi de type Helmholtz–Poisson, plutôt que celle d’une simple équation de Poisson : le vide continue de transmettre l’influence gravitationnelle à toutes les échelles, mais il la module de façon anisotrope selon sa propre élasticité.
On obtient ainsi une gravitation localement amplifiée mais globalement bornée, qui reproduit toutes les prédictions du premier ordre d’Einstein tout en régularisant naturellement les extrêmes d’énergie de champ.
prend alors la forme d’une loi de type Helmholtz–Poisson, plutôt que celle d’une simple équation de Poisson : le vide continue de transmettre l’influence gravitationnelle à toutes les échelles, mais il la module de façon anisotrope selon sa propre élasticité.
On obtient ainsi une gravitation localement amplifiée mais globalement bornée, qui reproduit toutes les prédictions du premier ordre d’Einstein tout en régularisant naturellement les extrêmes d’énergie de champ.
Un second aspect complète ce tableau : la saturation. À très haute densité — dans les étoiles à neutrons, les trous noirs ou toute région où le champ de cadence atteint son seuil — la réponse élastique du vide atteint son plafond. Au-delà de ce point, le champ ne peut plus approfondir son potentiel : sa rigidité est maximale, son élasticité s’effondre, et le milieu cesse d’absorber la contrainte. Le vide entre alors dans une phase de rupture, libérant sa tension stockée sous forme de rétablissement de phase — un processus observable sous forme explosive, sous la forme de sursauts d’énergie ou d’ondes gravitationnelles. Tel une membrane tendue jusqu’à la limite qui restitue une vibration brève, le vide rétablit sa cadence en restituant son énergie au sein de l’espace-temps. Dans ce cadre, l’accélération cosmique et la dynamique des objets compacts partagent une même origine : la tendance du vide à se saturer, se tendre, puis se détendre. L’espace n’accélère pas sous la poussée d’une mystérieuse énergie sombre : il respire, car le tissu du vide ne peut s’étirer indéfiniment.
Ces propriétés élastiques engendrent aussi des ondes — deux familles d’oscillations portées par le continuum du vide.
Les modes transverses de rigidité se propagent presque comme les ondes gravitationnelles d’Einstein,
tandis que les modes longitudinaux de cadence provoquent de subtiles dérives de fréquence, détectables par les interféromètres de haute précision et les réseaux d’horloges.
Le vide apparaît alors comme un milieu à la fois solide et résonant, capable de transmettre l’information sans frottement.
L’absence de traînée dans les mouvements célestes — planètes éternellement en orbite, photons glissant sans résistance — devient l’expression naturelle d’un écoulement laminaire à travers ce substrat rigide.
Là où la Relativité décrivait la courbure, le VGM explore l’acoustique du vide — un univers qui transporte non seulement la lumière, mais la résonance elle-même.
La beauté du tableau du vide élastique tient à sa cohérence d’échelle.
Le paramètre qui fixe la rigidité au laboratoire détermine aussi l’accélération cosmique ; le champ qui guide la chute des pommes règle également l’expansion des galaxies.
Sur le plan mathématique, cette unité se manifeste à travers l’opérateur trans-échelle ![]() , qui relie les constantes locales de cadence à la dérive cosmologique
, qui relie les constantes locales de cadence à la dérive cosmologique ![]() .
.
En langage physique : un champ, un rythme, à toutes les échelles.
Ainsi, lorsque nous voyons les galaxies s’éloigner plus vite que la géométrie ne le permet, nous ne contemplons peut-être pas que l’expansion d’un espace qui se dilate, mais aussi au relâchement d’une tension sous-jacente du vide — un retour à l’équilibre d’un vide mis sous contrainte il y a 13,8 milliards d’années.
Mettre la réalité à l’épreuve : le programme de falsification
“Peu importe la beauté d’une théorie, peu importe l’intelligence de celui qui la formule : si elle ne résiste pas à l’expérience, elle est fausse.” — Richard Feynman, Le caractère des lois physiques (1965)
Le Modèle de Gravité du Vide (VGM) se soumet à la même épreuve de vérification : chacun de ses paramètres correspond directement à une grandeur observable. Aucune constante cachée, aucun ajustement arbitraire — seulement un champ dont le comportement peut être mesuré par des horloges, de la lumière et des ondes.
Le modèle repose sur un ensemble compact de cinq quantités mesurables :
![]()
Chacune décrit un aspect précis du comportement du vide :
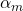 : l’universalité de la chute libre, testée par la comparaison entre masses atomiques et masses macroscopiques ;
: l’universalité de la chute libre, testée par la comparaison entre masses atomiques et masses macroscopiques ; 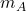 et
et 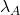 : la raideur et la portée du vide, contraintes par la déviation de la lumière et le délai de propagation ;
: la raideur et la portée du vide, contraintes par la déviation de la lumière et le délai de propagation ; 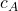 : la vitesse des ondes de rigidité, vérifiée par les détecteurs d’ondes gravitationnelles ;
: la vitesse des ondes de rigidité, vérifiée par les détecteurs d’ondes gravitationnelles ; 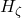 : la dérive cosmique de la cadence, mesurable par les relevés de décalage spectral et les comparaisons d’horloges sur des bases cosmologiques.
: la dérive cosmique de la cadence, mesurable par les relevés de décalage spectral et les comparaisons d’horloges sur des bases cosmologiques.
La force du VGM réside dans son protocole de falsification fermé :
cinq mesures suffisent à trancher sur la validité du modèle.
Si l’équivalence des horloges et de la matière est respectée (![]() ), si les ondes de rigidité se propagent à la vitesse de la lumière (
), si les ondes de rigidité se propagent à la vitesse de la lumière (![]() ), et si les coefficients post-newtoniens de premier ordre sont égaux (
), et si les coefficients post-newtoniens de premier ordre sont égaux (![]() ), alors le VGM passe les mêmes tests que la Relativité Générale.
), alors le VGM passe les mêmes tests que la Relativité Générale.
Mais il va plus loin : il prédit de légères déviations corrélées au second ordre — infimes différences dans le délai de Shapiro, la précession du périhélie ou les interférences d’onde — formant un schéma unique, mesurable et falsifiable.
Une seule incohérence parmi ces relations suffirait à réfuter l’hypothèse sans métrique.
Et il ne s’agit pas d’un simple exercice théorique, des expériences déjà réalisées atteignent la sensibilité requise.
- L’expérience radio Cassini a établi <img src="https://vacuumgravity.org/wp-content/ql-cache/quicklatex.com-40157c45fefd8add20b9fbe1df4a3c37_l3.png" class="ql-img-inline-formula quicklatex-auto-format" alt="|\gamma - 1| ;
- la Lunar Laser Ranging confirme <img src="https://vacuumgravity.org/wp-content/ql-cache/quicklatex.com-71ae65d83cce518748a9bdec3c56e39a_l3.png" class="ql-img-inline-formula quicklatex-auto-format" alt="|\beta - 1| ;
- les observatoires LIGO et LISA limitent <img src="https://vacuumgravity.org/wp-content/ql-cache/quicklatex.com-45769f5dfb067ef1829315682c07b70e_l3.png" class="ql-img-inline-formula quicklatex-auto-format" alt="|c_{A}/c - 1|
Les prochaines missions — SKA, ELT, BepiColombo — mesureront directement la dérive ![]() , capable de détecter une évolution de cadence inférieure à une centième du taux de Hubble.
, capable de détecter une évolution de cadence inférieure à une centième du taux de Hubble.
Ce ne sont plus des spéculations philosophiques, mais les frontières instrumentales de la physique moderne.
Pour relier ces observations à toutes les échelles, le VGM s’intègre aux solveurs cosmologiques standards (CLASS, CAMB), permettant au champ de cadence d’évoluer d’un contexte de laboratoire jusqu’à l’expansion cosmique dans un cadre unique.
En ce sens, il prolonge l’ambition einsteinienne : une même équation gouvernant tous les phénomènes gravitationnels, des horloges atomiques jusqu’à l’univers accéléré.
La différence est de nature : là où Einstein formulait une unité géométrique, le VGM propose une continuité métrologique, le même champ calibré par les mêmes grandeurs physiques à toutes les échelles.
Au terme de cette cohérence, seule la donnée expérimentale pourra trancher. Si aucune dérive de cadence n’est détectée, ou si les corrélations de second ordre (2PN) échouent, le modèle disparaîtra comme il se doit.
Mais si ne serait-ce qu’un seul des motifs qu’elle prédit venait à se manifester — un infime biais de fréquence, une dérive commune entre des horloges lointaines — cela pourrait signifier que la gravité n’est pas qu’une question de géométrie.
D’Einstein au vide : la continuité philosophique
Toute révolution scientifique commence par une relecture de l’évidence.
Newton transforma la chute des pommes en loi universelle ; Einstein convertit la force de gravitation en courbure de l’espace-temps.
Le Modèle de Gravité du Vide (VGM) s’inscrit dans cette filiation, non comme une rupture, mais comme un prolongement naturel : la question qui surgit une fois la géométrie de l’univers tracée. Si la courbure nous dit comment la matière se meut, le vide explique pourquoi elle se meut ainsi.
L’idée plonge ses racines dans la pensée du début du XXᵉ siècle.
Déjà, Ernst Mach suggérait que l’inertie ne provenait pas d’une propriété interne des corps, mais de leur interaction avec la totalité de la matière cosmique : que le mouvement local dépendait du ciel tout entier.
Einstein admira cette intuition, mais finit par la transmuter en géométrie: l’inertie ne résultait plus de la présence des étoiles, mais de la forme de l’espace-temps lui-même.
La idée philosophique était posée, le mouvement et la matière ne sont pas absolus, mais relationnels.
Dans le VGM, ce principe réapparaît sous une forme mesurable. Un champ de cadence ![]() agit comme un intermédiaire global transmettant l’inertie du cosmos au local.
agit comme un intermédiaire global transmettant l’inertie du cosmos au local.
Lorsqu’un corps résiste à l’accélération, il s’oppose à la rigidité du vide, à la tension de la cadence universelle.
Ainsi, l’inertie n’est plus un axiome, mais la réponse d’un milieu réel — celui-là même qui module la gravitation.
Cette vision restaure ce que la Relativité Générale avait laissé de côté : un substrat physique pour l’inertie et le temps.
Là où Einstein voyait la géométrie comme fondement, le VGM la considère comme un langage décrivant la propagation des signaux au sein d’un milieu.
Le champ ![]() n’est pas un potentiel abstrait de coordonnées, mais une propriété tangible du vide, reliant matière et lumière par une constante métrologique unique,
n’est pas un potentiel abstrait de coordonnées, mais une propriété tangible du vide, reliant matière et lumière par une constante métrologique unique,
![]()
Cette continuité entre gravitation, inertie et métrologie réalise une forme moderne du rêve de Mach : tout le cosmos participant à la définition du mouvement local, désormais à travers un champ expérimentalement testable.
Les implications philosophiques vont plus loin encore.
En ancrant la gravitation dans un champ mesurable plutôt que dans un postulat géométrique, le VGM réduit le fossé entre Relativité et physique quantique.
Le même vide qui héberge les fluctuations quantiques porterait aussi la structure que nous nommons espace-temps.
Ainsi, le modèle ne renie pas la vision d’Einstein : il la prolonge.
Les lois de la physique demeurent invariantes, mais leur scène se met à palpiter.
La géométrie devient émergente, non imposée ; la relativité, non plus ontologique, mais opérationnelle.
Le Modèle de Gravité du Vide (VGM) n’entend pas remplacer la vision d’Einstein, cependant, elle pourrait l’étendre au domaine de la mesure de précision, où la géométrie et la métrologie deviennent deux langages d’une même réalité.
Écouter le rythme de l’univers
La physique a toujours été un dialogue entre mathématiques et sens.
Les équations décrivent le monde, mais seule l’interprétation révèle ce que les symboles signifient.
Depuis un siècle, la géométrie d’Einstein nous a offert une image d’une précision inégalée : un univers qui se courbe, s’étire et ondule sous le poids de l’énergie.
Mais peut-être avons-nous confondu la carte et la musique.
La courbure est réelle, mais peut-être n’est-elle que le motif visible d’un battement invisible.
Le Modèle de Gravité du Vide (VGM) nous invite à écouter autrement.
Il nous suggère que la gravité n’est ni une main invisible tirant sur la matière, ni même une déformation de l’espace-temps, mais la modulation lente de la fréquence du vide.
Chaque horloge, chaque photon, chaque mouvement devient un acte de résonance avec cette cadence sous-jacente.
Là où la Relativité Générale nous apprenait à tracer la forme de l’univers, le VGM nous demande d’en mesurer le tempo.
Ainsi, il réconcilie la précision de la métrologie avec l’émerveillement de la cosmologie.
Ce passage du dessin au rythme n’est pas un simple jeu de langage : c’est une transformation philosophique. Il déplace la question « Qu’est-ce que l’espace-temps ? » vers « Que fait le vide ? ».
Un milieu silencieux et inerte devient un milieu vivant, capable de vibrer, de résister et d’évoluer. Sa rigidité expliquerait pourquoi les galaxies se maintiennent, pourquoi l’expansion s’accélère sans recourir à une énergie sombre ad hoc. Dans cette vision, la physique devient l’art de détecter d’infimes différences de cadence, l’art d’entendre la structure dans le silence.
Si ce cadre se vérifie, les conséquences seraient profondes.
- La géométrie que nous avons si patiemment cartographiée ne serait que l’ombre projetée par la dynamique interne du vide, et les lois de la gravitation émergeraient de la manière dont ce milieu rythme sa vibration.
- L’univers ne se contenterait plus d’exister : il jouerait — chaque oscillation de son vide participerait à une symphonie cosmique embrassant toutes les échelles.
- Nos instruments — horloges, interféromètres, télescopes — ne seraient plus seulement des détecteurs : ils deviendraient les microphones de cette musique fondamentale.
Peut-être alors que l’avenir de la physique fondamentale dépendra moins de la finesse avec laquelle nous mesurons les distances que de la précision avec laquelle nous comparons les fréquences — et comprendre la gravité, ce serait reconnaître que nous vivons au sein d’un vaste continuum résonant : un vide qui vibre pour nous raconter son histoire.
Épilogue — Un horizon ouvert
Le Modèle de Gravité du Vide (VGM) propose un nouvel angle de vue sur la gravitation. En révélant que l’espace ne se courbe peut-être pas, mais qu’il résonne, il transforme la physique en un dialogue entre mesure et sens. Chaque expérience devient un fragment du rythme de l’univers — une résonance entre la matière et le vide lui-même.
Mais derrière cette nouvelle harmonie se dissimulent des questions plus profondes :
- Si la gravité est l’effet d’un ralentissement de fréquence, qu’est-ce alors que la masse — un excès d’énergie condensé dans la matière ?
- Et la lumière — la manifestation visible des vibrations de ce même champ ?
- Et que signifie, pour le cosmos, d’orchestrer un espace vibrant d’une infinité de tempos ?
Chaque découverte dévoile une strate supplémentaire du réel, laissant entrevoir que la cadence du vide n’est peut-être que la première note d’une symphonie plus vaste.
Comprendre la gravitation, c’est peut-être apprendre à écouter le silence qui soutient toute chose.