Une Simplicité Oubliée
Imaginez-vous au sommet d’une montagne au lever du jour. Deux horloges atomiques battent la mesure : l’une posée à vos pieds, l’autre tenue à bout de bras. Toutes deux sont d’une précision extrême, identiques à l’atome près. Pourtant, à mesure que le soleil monte, elles se désynchronisent. Subtilement, celle tensynchronisent. Subtilement, celle ten\u00ue plus haut avance plus vite.
Ce décalage infinitésimal n’est pas une anomalie : il est au cœur de notre système GPS, des missions spatiales, et de la confirmation des théories d’Einstein. Mais si ce décalage n’était pas causé par une courbure de l’espace-temps ? Et s’il était simplement le reflet d’un changement de rythme du vide lui-même ?
La Question Oubliée
La physique actuelle explique le décalage gravitationnel par une géométrie courbe. Mais la géométrie, si élégante soit-elle, décrit ce qui se passe, plus qu’elle n’explique pourquoi. Et si nous retournions la question ?
Et si la gravitation était le vide ajustant sa cadence ?
Plutôt que d’imaginer des objets déformant une toile abstraite, concevons un milieu universel dont l’horloge interne ralentit ou s’accélère au voisinage de l’énergie. Dans ce tableau, la gravité n’est plus une courbure d’espace, mais une modulation locale du tempo du temps.
Un Vide Qui Bat
Le Modèle Gravitationnel du Vide (VGM) introduit un champ scalaire unique : le champ de cadence ![]() , qui décrit les variations locales de la fréquence interne du vide. Ce champ est défini par :
, qui décrit les variations locales de la fréquence interne du vide. Ce champ est défini par :
![]()
où ![]() est la fréquence nominale du vide oscillant, et
est la fréquence nominale du vide oscillant, et ![]() sa déviation locale due à la présence d’énergie ou de masse.
sa déviation locale due à la présence d’énergie ou de masse.
Dans ce cadre, un champ gravitationnel n’est rien d’autre qu’un gradient de cadence. Les horloges ralentissent là où ![]() augmente. La lumière se propage plus lentement dans les régions où le vide dilate son rythme. La courbure apparente des trajectoires devient une conséquence du passage à travers un paysage temporel non uniforme.
augmente. La lumière se propage plus lentement dans les régions où le vide dilate son rythme. La courbure apparente des trajectoires devient une conséquence du passage à travers un paysage temporel non uniforme.
Tel un tambour tendu, le vide réagit de manière élastique aux sollicitations d’énergie. La matière draine localement la cadence, et le champ ![]() redistribue cette tension pour maintenir l’équilibre inertiel. Même l’inertie devient un effet de cette dynamique scalaire.
redistribue cette tension pour maintenir l’équilibre inertiel. Même l’inertie devient un effet de cette dynamique scalaire.
Comment le Vide Imite la Géométrie
Pour reproduire les prédictions d’Einstein, ce champ scalaire doit rendre compte des phénomènes observés : décalage vers le rouge, déviation lumineuse, retard de Shapiro. Il le fait, via un indice de réfraction effectif de la lumière défini par :
![]()
Le potentiel gravitationnel ![]() devient
devient ![]() , et toutes les observations au premier ordre post-newtonien (1PN) sont automatiquement satisfaites.
, et toutes les observations au premier ordre post-newtonien (1PN) sont automatiquement satisfaites.
Les horloges atomiques envoyées en orbite mesurent directement ![]() . Les satellites GPS, en corrigeant ces variations, s’accordent déjà au rythme scalaire du vide. Le VLBI, les mesures de Shapiro, la lentille gravitationnelle : tous peuvent être reéxprimés comme des effets de réfraction sur le champ
. Les satellites GPS, en corrigeant ces variations, s’accordent déjà au rythme scalaire du vide. Le VLBI, les mesures de Shapiro, la lentille gravitationnelle : tous peuvent être reéxprimés comme des effets de réfraction sur le champ ![]() .
.
Le VGM n’est pas une alternative à la relativité générale : c’en est le jumeau opérationnel, formulé en langage scalaire plutôt que tensoriel.
Des Racines Anciennes
L’idée d’une gravitation émergeant du vide n’est pas neuve. Mach entrevoyait l’inertie comme un effet relationnel. Brans et Dicke proposèrent des champs scalaires gravitationnels. Sakharov entrevoyait l’élasticité de l’espace comme induite par les fluctuations du vide. Et Verlinde reformula la gravité comme une entropie effective.
Le VGM affine ces intuitions en leur donnant une base métrologique directe. Il fait de ![]() un champ observable, testable, unifiant les visions scalaires et émergentes dans un cadre commun.
un champ observable, testable, unifiant les visions scalaires et émergentes dans un cadre commun.
Le Vide en Tempo
Revenons au sommet de la montagne. L’accélération de l’horloge haute n’est pas un effet de hauteur, mais le vide respirant plus librement, dans un rythme gravitationnel plus rarefié. Le champ ![]() est cette respiration : une modulation silencieuse et omniprésente, qui sculpte orbites, retards et décalages.
est cette respiration : une modulation silencieuse et omniprésente, qui sculpte orbites, retards et décalages.
Nous avons longtemps observé comment les horloges réagissent à la gravité. Il est temps d’écouter ce que la gravité révèle du rythme du vide.
Chapitre de Consolidation
Et si la gravité était un battement, non une courbure ? Le Modèle Gravitationnel du Vide reformule la pesanteur comme un champ scalaire ![]() qui module le rythme du vide. Horloges et rayons lumineux réagissent aux gradients de ce champ, non à la géométrie. Les instruments métrologiques modernes mesurent déjà
qui module le rythme du vide. Horloges et rayons lumineux réagissent aux gradients de ce champ, non à la géométrie. Les instruments métrologiques modernes mesurent déjà ![]() directement. Le VGM offre une relecture scalaire, testable et élégante des phénomènes gravitationnels.
directement. Le VGM offre une relecture scalaire, testable et élégante des phénomènes gravitationnels.
Points Clés
- La gravité devient un champ scalaire
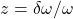 .
. - Les horloges ralentissent où
 croît, la lumière se réfracte.
croît, la lumière se réfracte. - L’indice
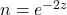 reproduit toutes les prédictions 1PN de la RG.
reproduit toutes les prédictions 1PN de la RG. - Le GPS, le VLBI et les horloges atomiques mesurent
 .
. - Le VGM unifie les approches scalaires, Machiennes et entropiques.
Pour Aller Plus Loin
- Fondements scalaires et redshift : (CE001)
- Propagation lumineuse et optique gravitationnelle : (CE003), (CE004)
- Calibration expérimentale : GPS, horloges, VLBI : (CE011a)
- Traduction GR/VGM : (CE016a), (CE016b)