“Perhaps the universe doesn’t curve — it keeps time.”
— Vacuum Gravity Model, 2025
We introduces the Vacuum Gravity Model (VGM) — a metric-free framework in which gravitation, inertia, and the flow of time arise from measurable variations of a single scalar field: the cadence of the vacuum.
Rather than curving spacetime, the vacuum changes its tempo.
General Relativity’s predictions emerge as first-order limits, while the model predicts finite-range rigidity and Born–Infeld-type cosmic acceleration.
It invites a shift from geometry to metrology: gravity becomes the comparison of rhythms rather than of shapes, suggesting that the universe may not curve — it beats.
The Beauty and the Limits of Curvature
For more than a century, General Relativity has stood as one of the most beautiful and successful ideas in science.
With a single geometric principle — “mass tells space how to curve, and space tells mass how to move” — Einstein turned gravity from an invisible pull into the very shape of reality.
From the dance of planets to the ripples of merging black holes, every prediction has matched observation with astonishing precision.
When astronomers confirm that gravitational waves travel at the speed of light, they are really confirming that geometry itself can vibrate.
And yet, behind that triumph hides a quiet question that Einstein himself never resolved: what is it that actually curves?
Relativity describes how space-time behaves, not what it is made of.
The theory gives geometry dynamical life but leaves the stage material undefined.
Between the smooth manifold of General Relativity and the quantum vacuum of field theory yawns a conceptual gap: geometry bends continuously, while the vacuum seethes with discontinuous fluctuations.
In the language of modern physics, the left hand of the universe is curved, the right hand is granular, and no one yet knows how they clasp.
This gap matters.
It shapes every paradox at the frontier of gravity and quantum mechanics — black-hole entropy, cosmic acceleration, the cosmological constant problem.
General Relativity succeeds wherever geometry is gentle, but it falters where the microscopic structure of space should reveal itself.
Its equations tell us how curvature responds to energy, but they do not tell us what physical property of the vacuum defines the pace of clocks, the path of light, or the inertia of matter.
To ask what curves is to ask what the vacuum itself is.
Perhaps, then, geometry was never the fundamental actor — only the language we use to describe a deeper phenomenon. The next step could be to look beneath the manifold — to search for a measurable substance of the vacuum, a field whose variations give rise to what we perceive as curvature.
If such a substrate exists, gravitation might not be the bending of space but the response of that invisible medium to energy and motion. The question that opens this new approach to gravity is simple and radical: Is space-time’s geometry only the shadow of the vacuum’s physical state
The Hidden Question: What Is the Vacuum Made Of?
If geometry is only the stage on which matter moves, then what is the stage itself built from?
In Einstein’s equations the answer is purely mathematical: space-time is a differentiable manifold whose curvature encodes gravity.
Yet modern physics whispers that the vacuum is not empty at all.
Quantum field theory fills it with restless energy — virtual particles flickering in and out of existence, condensates forming and dissolving within attoseconds.
This “quantum vacuum” behaves less like a void and more like an ocean whose surface tension defines what we call the laws of nature.
But here lies the paradox: the quantum vacuum should weigh billions of times more than the universe can tolerate.
If one adds up the zero-point energies of every known field, the resulting energy density is ![]() times too large.
times too large.
To make Einstein’s equations fit observation, cosmologists must insert a compensating constant — the infamous cosmological constant — arguably the most perplexing fine-tuning in modern physics.
It is as if the vacuum hums so loudly that the equations must be tuned to near silence just for galaxies to exist.
For decades, physicists have suspected that the missing key might not lie in a new particle, but in an as yet unknown principle — perhaps even in the vacuum itself.
The substrate of the vacuum may be anything but inert or frozen; it could instead be highly energetic, fluid, and dynamic, capable of stretching, oscillating, or relaxing like an elastic medium upon which matter, motion, and the very fabric of the universe might depend.
This question — what is the vacuum made of? — marks the boundary between the known and the speculative. From Sakharov’s “induced gravity” to Verlinde’s entropic models and superfluid analogies, every attempt has sought a physical origin for the metric itself.
The Vacuum Gravity Model (VGM) enters this lineage with a decisive step: it identifies a single, measurable scalar field whose local variations can reproduce all tested predictions of General Relativity while remaining fundamentally metric-free.
In this view, gravitation, inertia, and time are not properties of curved space, but responses of a structured vacuum to energy and motion.
Perhaps the deepest mystery of modern physics is not that spacetime curves, but that it echoes the heartbeat of the vacuum — like the cardiogram of a living universe. To understand gravitation, we must therefore learn not how the universe bends, but how its vacuum beats.
The Concept of Vacuum Cadence
Imagine that the vacuum itself possesses a rhythm — a silent oscillation that defines the pace of every clock and the inertia of every mass.
This is the core idea of the Vacuum Gravity Model (VGM): gravitation, inertia, and the flow of time all arise from local variations of a single measurable scalar quantity — the cadence field, usually denoted ![]() .
.
Rather than describing how geometry bends, the VGM describes how the vacuum’s internal tempo changes from point to point.
In simple terms, the cadence field ![]() measures the “inertial tension” of the vacuum.
measures the “inertial tension” of the vacuum.
Where ![]() increases, clocks tick more slowly and light waves stretch, mimicking the gravitational redshift we observe near massive bodies.
increases, clocks tick more slowly and light waves stretch, mimicking the gravitational redshift we observe near massive bodies.
Where ![]() decreases, time accelerates and light gains frequency.
decreases, time accelerates and light gains frequency.
Every gravitational potential, every acceleration, every curvature of trajectory can therefore be traced back to a gradient in this field.
In its weak limit, ![]() behaves exactly like the Newtonian potential divided by
behaves exactly like the Newtonian potential divided by ![]() , ensuring perfect agreement with all first–post-Newtonian tests of General Relativity.
, ensuring perfect agreement with all first–post-Newtonian tests of General Relativity.
From this perspective, gravity is no longer geometry — it is metrology.
A gravitational experiment becomes a comparison of rhythms rather than of shapes.
An atomic clock in orbit and one on Earth do not occupy different positions in curved space-time; they simply inhabit regions of slightly different vacuum cadence.
The equation a = ![]() then expresses the equivalence principle directly: all bodies, massive or massless, respond to the same scalar gradient because all share the same vacuum rhythm.
then expresses the equivalence principle directly: all bodies, massive or massless, respond to the same scalar gradient because all share the same vacuum rhythm.
Such a description has an unexpected consequence: it unifies gravitation, inertia, and time under one observable law.
Acceleration results from the spatial gradient of cadence, inertia from the vacuum’s resistance to changing its rhythm, and time dilation from temporal variations of that same field. The three pillars of classical physics — motion, mass, and duration — emerge as different manifestations of a single physical reality: the dynamics of the vacuum.
Operationally, this framework does not discard Relativity; it reproduces it at first order and extends it beyond. The geometric metric of Einstein becomes an effective descriptor, a convenient way of expressing how the cadence field influences clocks and rulers. But the true dynamical variable is ![]() , a field that can, in principle, be measured directly through networks of atomic clocks and light-time experiments.
, a field that can, in principle, be measured directly through networks of atomic clocks and light-time experiments.
Where Einstein draws curvature, VGM records frequency.
If confirmed, this shift would mean that gravity is not a deformation of space-time but a modulation of the vacuum’s internal frequency — a physical beat woven into every process of the cosmos.
The universe, in this view, does not curve; it keeps time !
From Geometry to Metrology: Measuring the Rhythm of Space
If gravity is a rhythm rather than a curvature, then physics becomes an art of listening.
The task is no longer to map geometric shapes but to compare the ticking of clocks, the oscillation of light, and the steady hum of the vacuum itself.
In this metrological view, every gravitational effect is a measurable difference in frequency — a shift of cadence between two regions of the same underlying field.
Einstein’s geometry already hinted at this.
The redshift of light near a massive body, the slowing of clocks on Earth compared with those on satellites, and the bending of starlight by the Sun all reveal a single fact: time does not flow uniformly through the universe.
In the Vacuum Gravity Model (VGM) this variation is not a deformation of coordinates but a physical modulation of the vacuum field ![]() .
.
Each clock, each photon, experiences the same rhythm, so that their relative drifts become direct probes of the field’s gradient.
To measure gravity, one does not need a metric tensor — only an exquisitely precise comparison of frequencies.
Modern physics has already built the instruments for such an approach.
Networks of optical and microwave clocks, linked by laser and radio signals, routinely detect time shifts smaller than one part in ![]() .
.
Space missions such as ACES, LATOR, and BepiColombo refine these measurements, transforming gravitational physics into a branch of precision metrology.
Within the VGM framework, each observable — redshift, light-time delay, light deflection, even cosmological drift — corresponds to one of five fundamental parameters of the vacuum:
![]()
Together they define the rigidity, propagation speed, and slow evolution of the vacuum’s cadence.
At first post-Newtonian order, the numbers match Einstein’s predictions exactly:
![]()
But beyond that threshold, the VGM introduces correlated second-order corrections — minute deviations in Shapiro delay, perihelion precession, and interferometric phase — that form a closed, falsifiable pattern.
No arbitrary constants, no extra dimensions: only the measurable elasticity of the vacuum itself.
In this sense, the model does not overthrow General Relativity; it calibrates it.
Such an interpretation has profound consequences for how we practice physics.
If geometry is replaced by cadence, then theory becomes indistinguishable from measurement.
Gravitational physics turns into the science of comparing clocks — from atomic ensembles in Earth orbit to spectral lines in distant galaxies.
A future map of gravity may look not like a curved grid of space-time but like a topographic chart of frequency, where altitude represents the local tempo of the vacuum.
So, when we measure time shifts, we are already mapping the universe’s topography of time. The next step is to test whether this pulse could truly calibrate gravity itself.
The Elastic Universe: Rigidity and Cosmic Acceleration
If the vacuum truly sets the rhythm of gravity, it must also possess texture — an ability to stretch, resist, and recover.
In the Vacuum Gravity Model (VGM), this property is called rigidity: a finite elastic response of the vacuum that transmits both local gravitational effects and the universe’s slow cosmic drift.
Where General Relativity treats the metric as perfectly flexible, the VGM endows the vacuum with a measurable stiffness, described by two key parameters:
![]() , the correlation length that defines how far a deformation of cadence can spread, and
, the correlation length that defines how far a deformation of cadence can spread, and ![]() , the propagation speed of rigidity waves.
, the propagation speed of rigidity waves.
This elasticity changes everything.
In the weak-field regime of the Solar System, the vacuum behaves as an almost perfectly flexible medium: its effective stiffness is extremely low, corresponding to an immense correlation length ![]() .
In this regime, the vacuum responds only slowly to stress — its gradients unfold over vast distances, and gravity appears smooth and nearly Newtonian.
The cadence field then propagates freely, like ripples on an ocean so wide that its tension cannot be felt.
.
In this regime, the vacuum responds only slowly to stress — its gradients unfold over vast distances, and gravity appears smooth and nearly Newtonian.
The cadence field then propagates freely, like ripples on an ocean so wide that its tension cannot be felt.
At larger scales — galactic and cosmological — that same parameter shortens as the vacuum becomes locally tense and stiffer: its gradients sharpen, its response quickens, and gravity intensifies — as if the tension of the vacuum were tracing, around extreme masses, the faint shadow of invisible matter.
The differential equation governing ![]() thus takes a Helmholtz–Poisson form rather than a pure Poisson one, meaning that the vacuum still transmits gravitational influence universally, but modulates it anisotropically according to its own elasticity. The outcome is a self-regulated gravity — locally amplified but globally bounded — that reproduces all of Einstein’s first post-Newtonian predictions while naturally regularizing the extremes of field energy.
thus takes a Helmholtz–Poisson form rather than a pure Poisson one, meaning that the vacuum still transmits gravitational influence universally, but modulates it anisotropically according to its own elasticity. The outcome is a self-regulated gravity — locally amplified but globally bounded — that reproduces all of Einstein’s first post-Newtonian predictions while naturally regularizing the extremes of field energy.
A second piece of the puzzle is saturation. At extreme densities — near neutron stars, black holes, or any region where the cadence field is driven to its limit — the vacuum’s elastic response reaches its ceiling. Beyond this threshold, the field can no longer deepen its potential: its rigidity is maxed out, its elasticity collapses to zero, and the medium ceases to absorb stress. The vacuum then enters a rupture phase, releasing its stored tension through phase restoration — a process manifested as bursts or gravitational waves. Like a membrane stretched to breaking point that releases a sharp vibration, the vacuum restores its cadence by emitting energy back into spacetime. In this picture, cosmic acceleration and compact-object dynamics share a common origin: the vacuum’s tendency to saturate, tense, and relax. Space does not expand or collapse arbitrarily; it oscillates within the limits of its own resilience.
These same elastic properties give rise to waves — two families of oscillations supported by the vacuum continuum. Transverse rigidity modes propagate almost identically to Einstein’s gravitational waves, carrying distortions of tension across space. Longitudinal cadence modes, subtler and slower, appear as frequency drifts detectable by precision interferometers and clock networks. Together they reveal the vacuum as a medium both solid and resonant, transmitting information without friction. The absence of drag in celestial motion — planets circling endlessly, photons gliding unimpeded — emerges as a natural consequence of laminar flow within this rigid substrate.
Where Relativity mapped curvature, the VGM traces the acoustics of the vacuum — a cosmos that carries not just light, but resonance.
The beauty of this elastic-vacuum picture is its coherence across scales.
The same parameter that defines rigidity in the laboratory also governs the acceleration of galaxies; the same field that guides a falling apple tunes the tempo of the cosmos.
In mathematical form, this unity appears through the cross-scale operator ![]() , which links the constants describing local cadence to the cosmological drift
, which links the constants describing local cadence to the cosmological drift ![]() .
.
In physical language: one field, one rhythm, all scales.
When we observe galaxies receding faster than geometry should allow, we may not be witnessing the expansion of space itself, but the release of an underlying tension in the vacuum. The apparent acceleration of the universe would then no longer be an external push, but the return to equilibrium of a vacuum strained 13.8 billion years ago.
Testing Reality: The Falsification Program
“It doesn’t matter how beautiful your theory is, it doesn’t matter how smart you are. If it doesn’t agree with experiment, it’s wrong.” — Richard Feynman, The Character of Physical Law (1965)
The Vacuum Gravity Model (VGM) was built with this principle at its core: every quantity that defines it can, in principle, be measured. There are no hidden constants, no adjustable parameters — only the observable behavior of the vacuum itself.
The model rests on a compact set of five measurable quantities:
![]()
Each defines one aspect of the vacuum’s behavior:
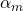 — the universality of free fall, tested by comparing atomic and macroscopic masses;
— the universality of free fall, tested by comparing atomic and macroscopic masses; 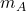 and
and 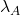 — the vacuum’s stiffness and range, constrained by light deflection and time-delay experiments;
— the vacuum’s stiffness and range, constrained by light deflection and time-delay experiments; 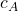 — the propagation speed of rigidity waves, verified by gravitational-wave detectors;
— the propagation speed of rigidity waves, verified by gravitational-wave detectors; 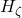 — the long-term drift of cosmic cadence, accessible through redshift-drift surveys and clock comparisons across cosmic baselines.
— the long-term drift of cosmic cadence, accessible through redshift-drift surveys and clock comparisons across cosmic baselines.
The power of this framework lies in its closed falsification protocol — a compact experimental design in which only five measurements decide the theory’s fate.
If the equivalence of clocks and matter holds (![]() ), if gravitational waves propagate at light speed (
), if gravitational waves propagate at light speed (![]() ), and if the 1PN coefficients match (
), and if the 1PN coefficients match (![]() ), then VGM passes the same precision tests that confirm General Relativity.
), then VGM passes the same precision tests that confirm General Relativity.
But the model goes further: it predicts small, correlated deviations at second post-Newtonian order — subtle shifts in Shapiro delay, perihelion precession, and interferometric phase — whose pattern is unique and measurable.
A single confirmed discrepancy among these relations would falsify the metric-free hypothesis.
This is not armchair speculation; current missions already probe the required sensitivity.
- The Cassini radio experiment constrained <img src="https://vacuumgravity.org/wp-content/ql-cache/quicklatex.com-40157c45fefd8add20b9fbe1df4a3c37_l3.png" class="ql-img-inline-formula quicklatex-auto-format" alt="|\gamma - 1|
- Lunar Laser Ranging confirms <img src="https://vacuumgravity.org/wp-content/ql-cache/quicklatex.com-71ae65d83cce518748a9bdec3c56e39a_l3.png" class="ql-img-inline-formula quicklatex-auto-format" alt="|\beta - 1|
- LIGO and LISA limit <img src="https://vacuumgravity.org/wp-content/ql-cache/quicklatex.com-45769f5dfb067ef1829315682c07b70e_l3.png" class="ql-img-inline-formula quicklatex-auto-format" alt="|c_{A}/c - 1| .
Forthcoming facilities — SKA, ELT, BepiColombo — will soon measure the redshift drift ![]() directly, detecting a cadence evolution as small as one part in
directly, detecting a cadence evolution as small as one part in ![]() of the Hubble rate.
of the Hubble rate.
These are not philosophical speculations but instrumental frontiers.
To make predictions across such scales, VGM integrates into standard cosmological solvers (CLASS/CAMB), allowing the cadence field to evolve from laboratory conditions to cosmic expansion within one framework.
In this sense, it mirrors Einstein’s ambition: one set of equations governing all gravitational phenomena, from atomic clocks to the accelerating universe.
The difference is that VGM expresses this unity not through geometry but through metrological continuity — the same field calibrated by the same physical quantities everywhere.
Ultimately, the model’s success or failure will be decided by data: if no cadence drift is detected, or if the 2PN correlations fail, VGM will vanish as it should.
But if even one of its predicted patterns were to emerge — a tiny frequency bias, a shared drift among distant clocks — it would mean that gravity is not merely a question of geometry after all.
From Einstein to the Vacuum: The Philosophical Continuity
Every revolution in physics begins as a reinterpretation of the obvious.
Newton turned falling apples into a universal law; Einstein turned the pull of gravity into the curvature of spacetime.
The Vacuum Gravity Model (VGM) follows that lineage, not as a rebellion but as a continuation — the next logical question once the geometry of the universe has been mapped. If curvature tells us how matter moves, the vacuum tells us why it moves that way.
The idea has deep roots.
In the early twentieth century, Ernst Mach suggested that inertia itself might arise from the influence of all matter in the cosmos — that local motion depends on the distant stars.
Einstein admired Mach’s intuition but ultimately replaced it with geometry: inertia emerged not from interaction with the universe but from the shape of spacetime itself.
Yet the philosophical seed remained: motion and matter are relational, not absolute.
In the VGM, this principle reappears in a measurable form. The vacuum field ![]() acts as the global intermediary that transmits inertia from the cosmos to the local.
acts as the global intermediary that transmits inertia from the cosmos to the local.
When a body resists acceleration, it is pushing against the rigidity of that field — against the cadence of the universe itself.
Through this lens, VGM restores something that General Relativity set aside: a physical substrate for inertia and time.
Where Einstein saw geometry as fundamental, VGM treats geometry as a language describing the propagation of signals within a medium. The field ![]() is not an abstract coordinate potential but a tangible property of the vacuum, linking matter and light through one metrological constant,
is not an abstract coordinate potential but a tangible property of the vacuum, linking matter and light through one metrological constant,
![]()
This continuity between gravitation, inertia, and metrology offers a modern realization of Mach’s dream — the entire cosmos participating in the determination of local motion, but now through an experimentally decidable field.
The philosophical implications reach further still.
By grounding gravity in a measurable field rather than a geometric postulate, the VGM narrows the gap between general relativity and quantum theory.
It suggests that the same vacuum which hosts quantum fluctuations also carries the structure we call spacetime.
In this sense, the model does not reject Einstein’s insight but fulfills it: the laws of physics remain invariant, but their stage gains a physical pulse.
Geometry becomes emergent, not imposed; relativity becomes operational, not ontological.
The Vacuum Gravity Model (VGM) does not replace Einstein’s vision; it may extend it into the domain of precision measurement, where geometry and metrology become two languages of the same reality.
Reflection: Listening to the Universe’s Rhythm
Physics has always been a dialogue between mathematics and meaning.
Equations describe the world, but only interpretation tells us what the symbols stand for.
For a century, Einstein’s geometry gave us the most precise description imaginable — a universe that curves, stretches, and ripples under the weight of energy.
Yet perhaps we mistook the map for the music.
The curvature was real, but it may have been only the visible pattern of a deeper, inaudible sound.
The Vacuum Gravity Model (VGM) invites us to listen differently.
It suggests that gravity is not an invisible hand pulling on matter, nor even a geometric deformation of spacetime, but the slow modulation of the vacuum’s own frequency.
Every clock, every photon, every motion becomes an act of resonance with that underlying cadence.
Where General Relativity taught us to draw the shape of the universe, the VGM asks us to measure its tempo. In doing so, it bridges the precision of metrology with the wonder of cosmology.
This shift from shape to rhythm is more than semantic; it is philosophical. It transforms the question “What is spacetime?” into “What does the vacuum do?”
It replaces the silent manifold with a medium that vibrates, resists, and evolves — a medium whose rigidity explains why galaxies hold together and why the cosmos accelerates without invoking dark energy. In this vision, physics becomes the art of detecting infinitesimal differences in cadence, the craft of hearing structure in silence.
If this framework were to prove true, its implications would be profound.
- The geometry we have so carefully mapped would reveal itself as a shadow cast by the vacuum’s own dynamics, with the laws of gravitation emerging from the way that medium keeps time.
- The universe would not merely exist; it would perform — each oscillation of the vacuum adding its note to a cosmic symphony that spans all scales.
- Our instruments — the clocks, interferometers, and telescopes — would be its microphones, recording the faint music of the real.
Perhaps, then, the future of fundamental physics will depend not on how finely we can measure distance, but on how precisely we can compare rhythms. To understand gravity might be to realize that we live inside a vast, resonant continuum — a vacuum that sings — and that every observation, every experiment, every heartbeat of a clock is a fragment of that eternal melody.
The question would no longer be how space bends, but how deeply the vacuum can sing.
Epilogue — The Open Horizon
The Vacuum Gravity Model (VGM) proposes to reframe the story of gravitation. By revealing that space may not bend but resonate, it turns physics into a dialogue between measurement and meaning. Each experiment listens to a small fragment of the universe’s rhythm — the resonance born from the meeting of energy, matter, and the vacuum itself.
Yet behind this new harmony lie deeper questions. If gravity is the effect of a slower rhythm, then what is mass — a lost tempo condensed into tangible matter? And what is light — a visible vibration of the same field? What does it mean for a cosmos to keep time with itself? Each discovery opens another layer of the real, suggesting that the cadence of the vacuum may be only the first note of a greater symphony still unfolding.
To understand gravity is perhaps to learn how to listen to the silence that sustains everything.